Les systèmes hamiltoniens à ports : un paradigme moderne pour la modélisation, la simulation, l’optimisation et la régulation de processus dynamiques
Qu’est-ce qui influence la dynamique ?
Il est possible de répondre à cette question en examinant par exemple les bilans énergétiques. La dissipation d’énergie dans l’environnement ou les flux d’énergie entre les différents composants du système sont en effet d’une importance capitale. De telles considérations permettent d’obtenir ce que l’on appelle des systèmes hamiltoniens à ports. Il s’agit de systèmes d’équations différentielles fortement structurés présentant de nombreuses propriétés avantageuses. Par exemple :
- les systèmes hamiltoniens à ports sont automatiquement stables et passifs ;
- le couplage de plusieurs systèmes hamiltoniens à ports aboutit à un système hamiltonien à ports global ;
- différents domaines de la physique (par exemple l’électrodynamique ou la mécanique) peuvent être facilement combinés, ce qui permet un traitement uniforme des systèmes multiphysiques.
En plus de l’analyse des propriétés de tels systèmes, le développement d’algorithmes de simulation, d’optimisation et de régulation exploitant ou préservant la structure joue un rôle très important dans la recherche. Il s’agit là de thématiques de recherche traitées à UniDistance Suisse.
Réduire les systèmes afin de mieux les comprendre
Les systèmes hamiltoniens à ports rencontrés dans la pratique sont souvent décrits par un très grand nombre de variables et donc très complexes, de sorte que la simulation, l’optimisation et la régulation sont extrêmement chronophages. Il est donc nécessaire d’extraire la partie dominante de la dynamique à l’aide de méthodes de réduction de modèle automatisées afin d’obtenir un système hamiltonien à ports réduit avec un très petit nombre de variables descriptives. Cela peut être réalisé, par exemple, par une approche basée sur les données dans laquelle la réponse du système à des excitations à différentes fréquences est calculée ou mesurée. Cela conduit à une nouvelle classe de méthodes de réduction de modèles basées sur l’optimisation et sur l’adaptation de données à un système dynamique de structure et de dimension données. Il a notamment été démontré que pour une même dimension réduite du système, il est possible d’obtenir des modèles réduits nettement plus précis qu’à l’aide des procédés de réduction de modèles connus qui conservent la structure.
Développement de régulateurs
Un autre point fort est le développement de régulateurs pour les systèmes hamiltoniens à ports, par exemple pour obtenir un comportement souhaité du système à l’aide de données de mesure en fonctionnement. Une catégorie de régulateurs est celle des régulateurs dits H-infini, dont l’objectif est de rendre le système régulé aussi insensible que possible aux influences perturbatrices extérieures non mesurables et aux erreurs de mesure. Dans le cas des systèmes hamiltoniens à ports, il est possible d’exploiter la structure et d’atteindre cet objectif par le biais d’un couplage avec un régulateur hamiltonien à ports, de sorte que le système couplé possède certaines propriétés de stabilité, ne serait-ce que par sa structure. Les résultats montrent une performance similaire par rapport à d’autres algorithmes établis, mais la nouvelle approche présente également des caractéristiques prometteuses pour le traitement de problèmes de dimension supérieure. Dans ce contexte, il est également prévu d’intégrer le traitement d’incertitudes de modèle supplémentaires dans la procédure de conception du régulateur.
D’autres pistes d’études possibles ?
De nombreuses questions restent ouvertes dans ce domaine. Par exemple, les modèles réduits pourraient également être déterminés par des simulations de systèmes en combinaison avec des méthodes d’apprentissage automatique. Cela comprendrait par exemple le traitement de dynamiques non linéaires ou l’intégration de grandeurs stochastiques. Une autre direction de recherche consiste en l’assimilation de données de systèmes hamiltoniens à ports, c’est-à-dire la mise à jour du système réduit pendant la durée du processus réel par des données mesurées. Cela permettrait par exemple de calculer, sur la base d’un modèle, des signaux de régulation plus précis pendant la durée du processus.
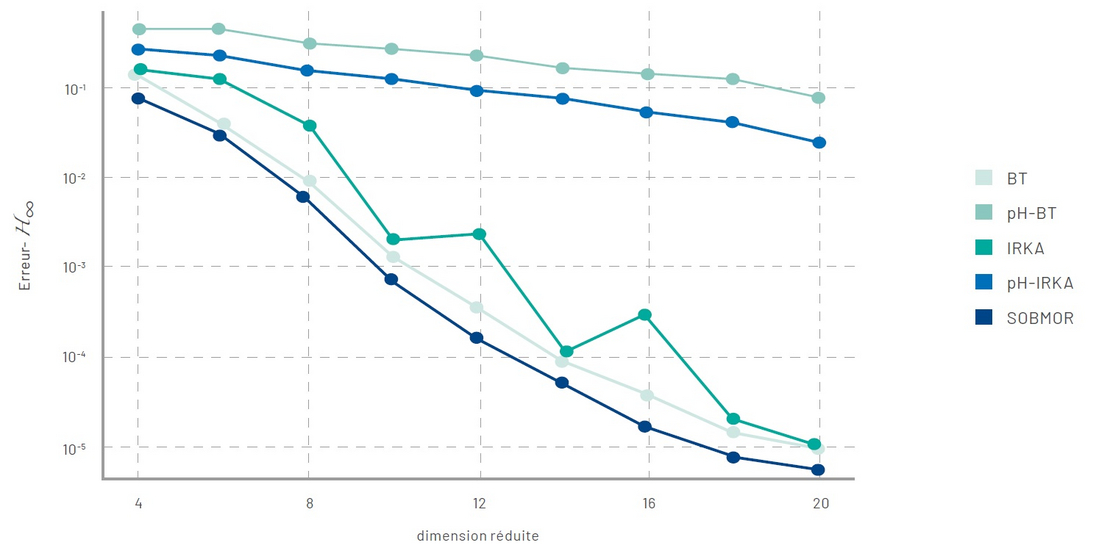
La nouvelle approche SOBMOR donne des résultats de réduction nettement meilleurs que les autres méthodes de conservation de la structure (pH-BT, pH-IRKA) et même que les méthodes génériques (BT, IRKA) qui ne conservent pas la structure.
Matthias Voigt

Matthias Voigt est professeur assistant au sein de la Faculté de mathématiques et informatique depuis 2021 et enseigne dans le cadre du Bachelor en mathématiques.
Son groupe de recherche s’intéresse principalement aux questions de la théorie mathématique des systèmes, plus particulièrement au développement de procédures automatisées pour réduire la complexité des systèmes dynamiques.
Matthias Voigt a lancé, en collaboration avec le professeur Thomas Mettler, une série de colloques en ligne (UniDistance Suisse Mathematics Colloquium) afin de mieux faire connaître la Faculté de mathématiques et informatique. Ces conférences s’adressent à un public spécialisé.
Autres actualités

[Etudiants] Conseils techniques pour se préparer à un examen en ligne
Lire la suite
Lehrbeauftragte oder Lehrbeauftragter für das Modul «M07 Persönlichkeit und Differentielle Psychologie, 10 ECTS» (18%)
UniDistance Suisse Lire la suite

L’adhésion à l’EUA renforce le positionnement international d’UniDistance Suisse
UniDistance Suisse Lire la suite
